本記事について
本記事は,以下の流れで説明する多変量正規分布の確率等高線の書き方についての,平均ベクトルの統計的仮説検定と,確率等高線の関係性を説明する記事です.
- 何をやろうとしているか?(こちらから)
- 多変量正規分布の平均ベクトルの統計的仮説検定(本記事)
- 実際に書いてみる(別記事:リンクを後で入れる)
- 読むのに必要とされる数学の補足
多変量正規分布の平均ベクトルの統計的仮説検定
定理1|マハラノビス距離の従う分布
$p$次元確率変数ベクトル$X$が平均$\mu$,正定値対称の分散共分散行列$\Sigma$の多変量正規分布に従う時,マハラノビス距離$T$は自由度$p$の$\chi^2$分布に従う.つまり,以下が成立する.
$$T:=(X-\mu)’\Sigma^{-1}(X-\mu) \sim \chi^2_p$$
定理1の証明
まず,$X\sim MN(\mu, \Sigma)$だから,$X-\mu \sim MN(0_p, \Sigma)$であること,また,$\Sigma$は正定値対称だから,ある直交行列$P$を用いて,
$$P’\Sigma P = D$$
のように,対角成分が正である対角行列へと対角化可能であることに注意する.この時,$\Sigma^{-1} = PD^{-1}P’$である.
ここで,$Z\sim MN(0_p, I_p)$なる,多変量標準正規分布に従う確率変数ベクトル$Z$を導入すると,
$$\begin{align}E[PD^{1/2}Z] &= PD^{1/2}E[Z] = 0_p\\ V[PD^{1/2}Z] &= PD^{1/2}V[Z]D^{1/2}P’ = PDP’ = \Sigma\end{align}$$
である.正規分布の性質より,$PD^{1/2}Z$は$X-\mu$と同様に$MN(0_p, \Sigma)$に従う.よって,マハラノビス距離の$X-\mu$を$PD^{1/2}Z$で置き換えることができ,それにより,
$$\begin{align}T &= (X-\mu)’\Sigma^{-1}(X-\mu)\\ &= (PD^{1/2}Z)’\Sigma^{-1}(PD^{1/2}Z)’\\ &= Z’D^{1/2}P’PD^{-1}P’PD^{1/2}Z = Z’Z = \sum_{j=1}^p z_j^2\end{align}$$
となることが確かめられる.ここで,$Z$は多変量標準正規分布に従うことから,$z_j\overset{i.i.d}{\sim}N(0,1),\space j=1,…,p$であり,$\chi^2$分布の定義から,$T=\sum_{j=1}^pz_j^2$は自由度$p$の$\chi^2$分布に従うことがわかる.$\square$
平均ベクトルの検定に向けて
さて,以上により,平均ベクトルの関数である検定統計量と,それが従う分布がわかりました.一般の検定論と同じように,平均ベクトルの検定も有意水準を$\alpha$として
$$Pr(T>c) = \alpha$$
となる$c$を定めて,検定統計量がそれより大きい場合に帰無仮説を棄却するという方法でよさそうです.上記の結果から,マハラノビス距離の標本から計算されるバージョンを定義して,自由度$p$の$\chi^2$分布の上側確率が$\alpha$となる点と大小関係を比較することで,平均ベクトルの検定が実施できそうなことが予想されます.実際
$$Pr(T>\chi^2_p(\alpha)) = \alpha$$
が成り立つことから,後は$T$を帰無仮説を真としたとき,標本平均ベクトルから定義すれば良いです.ただし,上記で$\chi^2_p(\alpha)$は自由度$p$の$\chi^2$分布の上側確率が$\alpha$となる点です.
平均ベクトルの検定
帰無仮説$H_0$が$\mu = \mu_0$,対立仮説$H_1$が$\mu\ne\mu_0$であるとする.また,真の$\Sigma$は既知とする.この時,帰無仮説が真という条件のもとでの検定統計量は
$$T = (\bar{X}-\mu_0)’\Sigma^{-1}(\bar{X}-\mu_0)\sim\chi^2_p$$
であり,
$$Pr(T \ge \chi_p^2(\alpha)) = \alpha$$
が成り立つことから,$T > \chi_p^2(\alpha)$の時,帰無仮説を棄却すれば良い.
$\Sigma$が未知のケース
$\Sigma$が未知の場合,その標本共分散行列$\hat{\Sigma}$を用いて,
$$T^2 := N(\bar{X}-\mu_0)’\hat{\Sigma}^{-1}(\bar{X}-\mu_0)$$
なる統計量を用いて,検定を実施すればよいです.この統計量をHotellingの$T^2$統計量とよびます.詳しくは,wikiをご確認ください.
多変量正規分布の確率等高線と平均ベクトルの統計的仮説検定のつながり
多変量正規分布の密度関数は,
$$\begin{align}f(x) &= \frac{1}{(2\pi)^{p/2}det(\Sigma)^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^t\Sigma^{-1}(x-\mu)\right)\\ &= const \times \exp\left(-\frac{1}{2}(x-\mu)^t\Sigma^{-1}(x-\mu)\right)\end{align}$$
であることから,指数部の中身$=$平均$\mu$からのマハラノビス距離により確率が定まることがわかります.つまり,ここの値がある値となる$x$を集めることで等高線が描画できます.
また平均ベクトルの検定は,突き詰めるとマハラノビス距離(もしくは似た定義のHotellingの$T^2$統計量)が
$$T = (X-\mu)’\Sigma^{-1}(X-\mu) > \chi^2_p(\alpha)$$
となった場合に,帰無仮説を棄却する手順でした.裏返すと,受容域$T<\chi_p^2(\alpha)$に対して,$Pr(T<\chi_p^2(\alpha)) = 1-\alpha$となります.つまり,
$$T = (X-\mu)’\Sigma^{-1}(X-\mu) = \chi_p^2(\alpha)$$
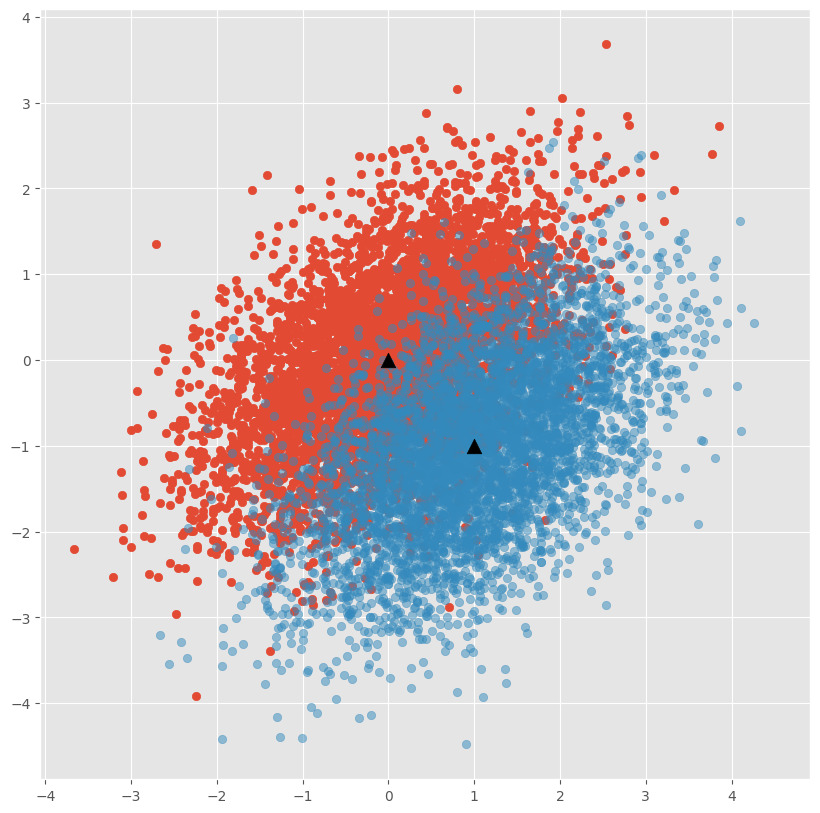
となる$X$を集めることで楕円がかけます.検定統計量を$\mu$からの距離としてみると,$Pr(T<\chi_p^2(\alpha)) = 1-\alpha$より,散布する$X$が$T<\chi_p^2(\alpha)$に入る確率が$1-\alpha$になると解釈できます.これを踏まえると,$T=\chi_p^2(\alpha)$となる$X$を集めた楕円は,$\mu$を中心として散布する$X$の確率$1-\alpha$の等高線を意味することがわかります.
まとめ
本記事では,「多変量正規分布の平均ベクトルの統計的仮説検定」と「平均ベクトルの仮説検定の検定統計量と確率等高線の関係」についてご説明しました.次の記事ではいよいよ,確率等高線を描いてみようと思います.(その前に前提としている数学の知識(ex. 高校数学←私が忘れていたため)を補足とした記事を先に書くかもです)
記事の中での誤りがございましたら,やんわりとご指摘ください.
読者様の参考になると幸いです.
コメント