本記事について
本記事は,以下の流れで説明する多変量正規分布の確率等高線の書き方について,前提とされる数学の知識(主に私が思い出さないといけなかったもの中心)を補足するものです.
前提知識|高校数学
弧度法
プログラムの引数では角度を指定する場合もあります.その際に,度数法と弧度法のどちらかが要求されるため,両方を互いに変換する式を覚えておくと良いです.弧度法の1ラジアンの定義は以下の通りです.
$$1rad = \frac{180^{\circ}}{\pi}$$
これを使って度数→ラジアンへ変換しましょう.逆に,ラジアン→度数に変換する場合は,
$$1^{\circ} = \frac{\pi}{180}\times 1rad$$
で変換しましょう.
図形と方程式・媒介変数表示・極座標表示
プログラムで図形を描画する際は,グラフと同様に座標の点を求めることが必要です.その際に,図形の方程式から値を求めることが要求されます.これは,高校数学で勉強した図形と方程式分野に関連しています.
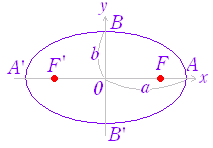
今回の一連の記事では,楕円の描画であるため,まずは楕円の方程式を振り返りましょう.画像のような楕円は以下の方程式で表されます.
$$\frac{x^2}{a^2} + \frac{y^2}{b^2}=1$$
$a$が$x$軸の長さ,$b$が$y$軸の長さを表しています.$a:b = 1:1$の時は正円になります.詳しくは,画像の引用元のページをご参照ください.
楕円をプログラムで描画するには,楕円の線上の$x,y$座標がわかれば良いのですが,上記の楕円の方程式を$x$(もしくは,$y$)について解くと,1つの$x$に対し,2つの$y$が対応します.そうなると配列の作り方,持たせ方が面倒になります(と私は感じました).そこで,角度$\theta$を媒介変数とし,直交座標系を極座標表系に対応づけることを考えましょう.直交座標$(x,y)$と極座標$(r,\theta)$は,
$$\begin{align}x &= r\cos\theta\\y &= r\sin\theta\end{align}$$
のような関係があります.この関係を用いると,$r=1$として,$\theta$を$0$から$2\pi$の範囲で動かすことで,1つの$\theta$に対して,円の方程式の円上の1つの$(x,y)$座標が得られます.そのため,配列としての持たせ方も単純です.楕円の場合も,
$$\begin{align}x &= a\cos\theta\\y &= b\sin\theta\end{align}$$
とおくことで,$\theta$に対して,楕円上の$(x,y)$座標が求まります.
(極座標は,線分の長さとx軸からの角度で定まる座標系だったので,人によっては複素数平面と対応づけて考えた方がイメージが膨らみやすいかもしれませんね.)
前提知識|大学数学
固有値分解
固有値分解を説明する前に,固有値,固有ベクトルについてご説明します.ある正方行列$A$(簡単のために正定値対称とします)の固有値と固有ベクトルは,
$$Ap = \lambda p$$
となるような長さ$1$のベクトル$p$とスカラー$\lambda$のことです.これらの$p,\lambda$はプログラムで求められることができるので,詳しい求め方は線形代数の教科書をご参照ください.
以上のような方程式を図示すると,以下の画像のようになります.ここで,黒色の矢印が,長さ1のベクトル,黒色の矢印を$\lambda$倍したものが青色の矢印です.つまり,$Ap=\lambda p$の式の解釈としては行列$A$を作用させた後,向きが変わらず長さだけが変わるベクトルが固有ベクトル$p$,その縮尺の変換量が固有値$\lambda$ということになります.
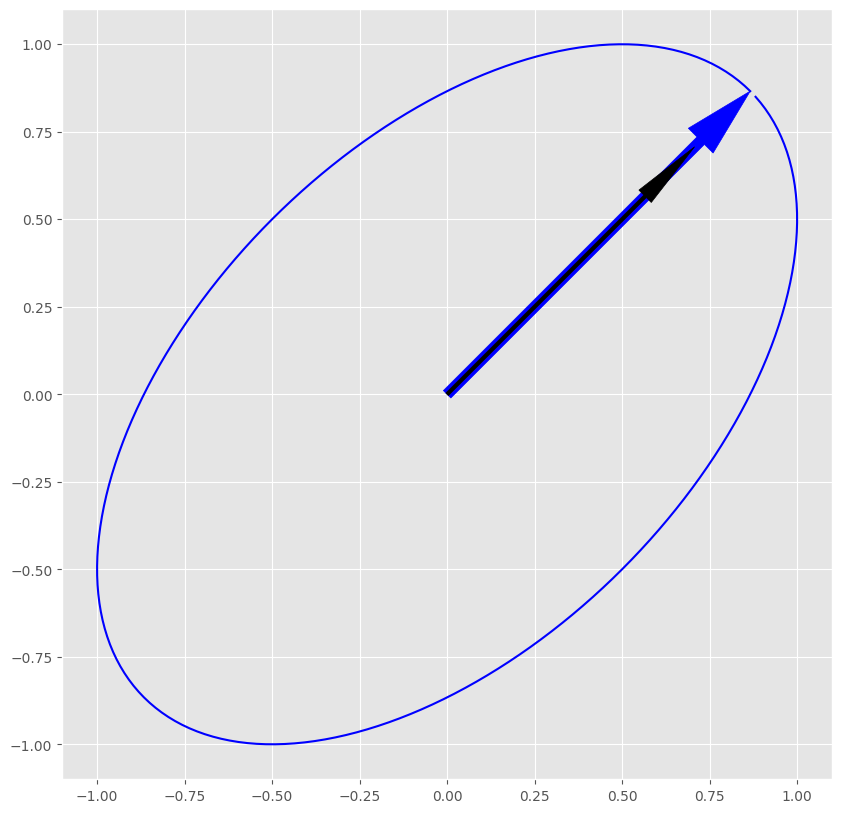
固有値分解は,第1固有ベクトルと直交するように第2固有ベクトルをとり,第1,2固有ベクトルと直交するように第3固有ベクトルをとり,,のように全ての固有ベクトルが直交するようにベクトルをとり,それに対応する固有値を求めることで得られます.そのような分解を
$$A = P\Lambda P’$$
のように書きます.
行列の掛け算と回転・縮尺のイメージ
特定の行列をかけるとベクトルはどのように変化するのでしょうか.今回は,対角行列$D$と回転行列$R$を取り扱って実際に見てみましょう.2次元ベクトル$x=(1,1)’$にそれぞれの行列をかけてみます.以降,元のベクトル$x$は黒矢印,変換後のベクトルは青矢印で表します.
対角行列$D$の場合
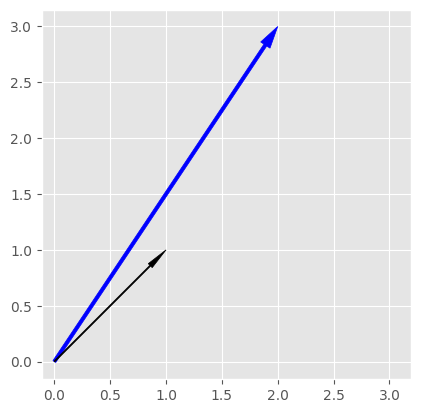
対角成分が2,3の対角行列をかけた場合が,以下のようになります.$x$軸に関して2倍,$y$軸に関して3倍した位置にベクトルが引き伸ばされています.対角行列は対応する軸の伸縮操作に対応します.
回転行列$R$の場合
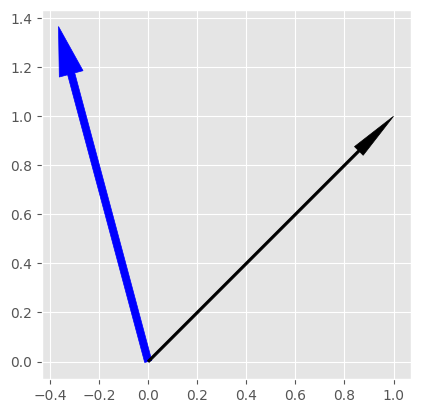
$60^\circ$回転させるための回転行列$R$を用いて変換すると,当然元のベクトルの長さを保ったまま$60^\circ$の位置に移動しています.回転行列はその名の通り,回転操作に対応しています.
まとめ
本記事では,多変量正規分布の確率等高線を描画する方法の一連の記事の中で,必要とされる数学の知識について,(私の思いだしを兼ねて)記載しました.これらの知識は特にプログラム上で等高線を描画する際に必要となります.
ひとえに等高線を描く,と言っても高校で学んだ数学から,大学で学ぶ線形代数・数理統計・多変量解析まで,さまざまな分野の知識を横断的に使うため,とても楽しい題材だなぁ,と感じています.
記事の中での誤りがございましたら,やんわりとご指摘ください.
読者様の参考になると幸いです.

コメント