本記事について
本記事は,以下の流れで説明する多変量正規分布の確率等高線の書き方についての,全体像を概観するための記事です.特に,何をやろうとしているか?についてのイメージ共有に絞って記載します.
多変量正規分布の平均ベクトルの検定統計量と楕円の式の関係
多変量正規分布の平均ベクトルの統計的仮説検定でご説明した通り,多変量正規分布の確率等高線は,
$$T = (X-\mu)’\Sigma^{-1}(X-\mu) = \chi_p^2(\alpha)$$
です.これをよく知っている楕円の方程式に帰着させましょう.今回は2変量正規分布を考えるため,カイ二乗分布の上側確率5%点は,分布表から$\chi_2^2(0.05) = 5.991$です.両辺をこの値で割ると,
$$(X-\mu)’\left(\frac{1}{5.991}\Sigma^{-1}\right)(X-\mu) = 1$$
となります.ここで,$\Sigma$の固有値分解を$\Sigma = PDP’$とすると,上式は,
$$\begin{align}&(P'(X-\mu))’\left(\frac{1}{5.991}D^{-1}\right)(P'(X-\mu)) = 1\\ &Y’\left(\frac{1}{5.991}D^{-1}\right)Y = 1\end{align}$$
とかけます.ここで,$(y_1, y_2) = Y:=P'(X-\mu)$とおきました.上式のベクトル表現を展開すると,
$$\frac{y^2_1}{\left(\frac{5.991}{d_1}\right)^2}+\frac{y^2_2}{\left(\frac{5.991}{d_2}\right)^2}=1$$
とかけることから,楕円の方程式に一致していることがわかります.あとはこれをもとに$y_1, y_2$を求めて楕円を書けば良いです.
今回はもっと簡便にかける方法をご紹介します.等高線の方程式
$$(X-\mu)’\left(\frac{1}{5.991}\Sigma^{-1}\right)(X-\mu) = 1$$
にて,$z = \frac{1}{\sqrt{5.991}}D^{-1/2}P'(X-\mu)$とおくと,等高線の方程式は,
$$1=z’z=z_1^2 + z_2^2$$
と正円の方程式に帰着させられます.これの逆を辿ると,$(X-\mu) = \sqrt{5.991}PD^{1/2}z$となることから,正円の円上の座標を対角行列$D^{1/2}$,回転行列$P$,引き伸ばしのスカラー$\sqrt{5.991]$を順にかけて変換することで,楕円の円上の座標を得られます.まとめると,,,
楕円の書き方はまとめると以下の通り.半径1の正円の座標$z$を$\Sigma=PDP’$を用いて
$$v = \sqrt{\chi_2^2(\alpha)}PD^{1/2}z$$
と変換すれば得られる.
となります.これを使って実際にプログラムで書いてみましょう!
プロットのためのスクリプト
プロットのためのスクリプトは以下の通りです.以下を実行することで,コードブロックの下の95%信頼領域を記載することができます.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import scipy
plt.style.use("ggplot")
chi2 = 5.99 # 自由度2のχ二乗分布の上側確率95%点
np.random.seed(123)
# 平均(0,0), 分散共分散行列[[1,0.5],[0.5,1]]の2変量正規分布から5000サンプル抽出する
mu = np.array([0.0,0.0])
Sig = np.array([[1,0.5],
[0.5,1]])
data1 = np.random.multivariate_normal(mean=mu, cov=Sig, size=5000)
## 等高線を描くための固有値分解
evd_res = np.linalg.eig(Sig) # Sig = PD^2P^tの固有値分解を実行
P, D = evd_res[1], np.diag(np.sqrt(evd_res[0]))
n = 200 # x,yを極座標に変換する際の,媒介変数の細かさの指定.今回は0~2piを200分割する.
t = np.arange(0,2*np.pi, 2*np.pi/n) # 媒介変数
# x, yを極座標表示して,半径1の正円の点を作成する
xy = np.array([np.cos(t), np.sin(t)])
#plt.plot(xy[0], xy[1]) # ほんまに正円か?と気になる方はコメントアウトを外してみてみてください.
# xyを変換して,95%信頼領域の外縁を作成する
xy2 = np.sqrt(chi2)*P@D@xy # <-- まとめると~のところの変換
fig, ax = plt.subplots(1,1, figsize=(10,10))
ax.plot(xy2[0], xy2[1], c="blue")
ax.scatter(data1[:,0], data1[:,1], color="black")
plt.axis("square")
plt.show()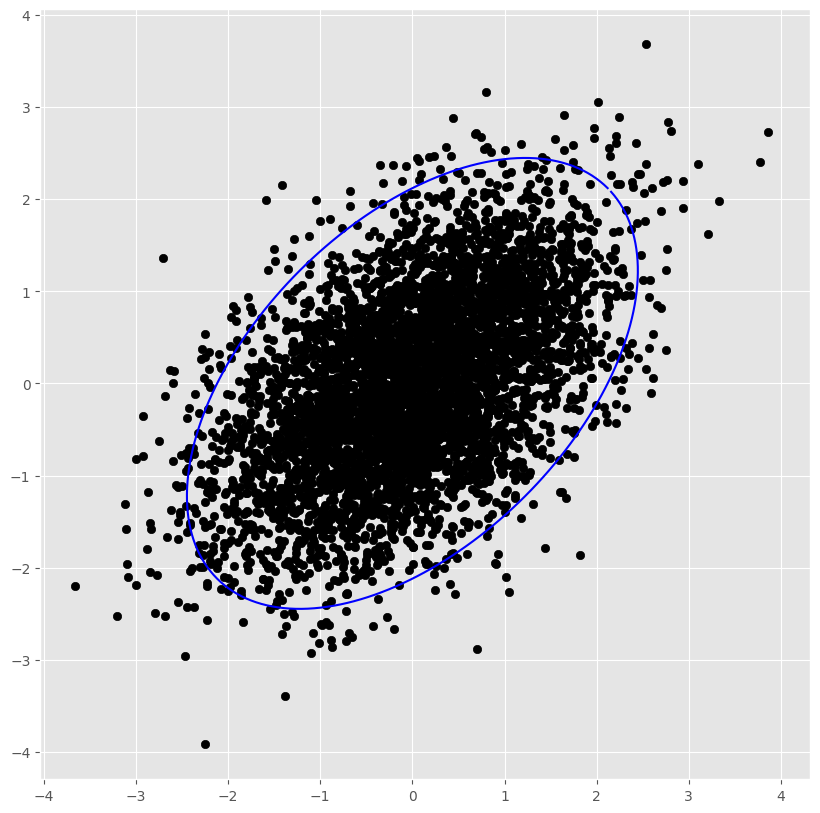
まとめ
本記事では,2変量正規分布の$\alpha$%信頼領域の等高線を記載するスクリプトについてご紹介しました.ここまでの一連の記事にて確率等高線がかけるようになったと思います.
記事の中での誤りがございましたら,やんわりとご指摘ください.
読者様の参考になると幸いです.
コメント