本記事で紹介されている内容
本記事では,下記の2点を紹介します.
- 応答変数が計数データである場合に利用可能な回帰モデルであるポアソン回帰の概要
- statsmodel.apiを用いて,pythonでポアソン回帰を実行する方法
ポアソン回帰/対数線形モデルとは
ポアソン回帰とは,「0,1,2,3,…のように離散的な整数値をとる応答変数に対する説明変数が持つ影響をモデリングする際に用いられるモデル」です.この応答変数のようなデータを計数データやカウントデータと呼ぶこともあります.以下,順を追って説明します.
一般化線形モデルの概要(正規線形モデルから始めて.フワッと)
「回帰」は,いくつかの説明変数を組み合わせて,応答変数がどのような値になるかを表現することを目的としています.回帰を行うモデルに属する正規線形モデル(通常の重回帰分析)では,応答変数は\((-\infty, \infty)\)の範囲の値をとると仮定されていました.これを数式で書くと,
$$y = x^t\beta + \epsilon,\ \epsilon\sim N(0,\sigma^2)$$
のようになります.ここで,\(y\)は応答変数,\(x=(1,x_1,x_2,…,x_p)^t\)は説明変数ベクトル,\(\beta=(\beta_0, \beta_1,…,\beta_p)^t\)は説明変数の係数(応答変数への寄与の大きさ,とでも解釈いただければと思います)を表しています.この式は,応答変数は説明変数の線型結合(重み付き和)で表される,と仮定しています.
\(\beta\)の係数が正と仮定する(このようにしても以下の議論での一般性は失われません)と,ある説明変数の値を無限に大きくすることで,応答変数の値を際限なく大きくすることができます.これは,冒頭に記載した通り,応答変数は\((-\infty, \infty)\)の範囲の値をとりうるということに対応しています.一方で,現実世界のデータでは,サッカーのゴール数など,応答変数の範囲が0,1,2,3,…のように離散的な整数値となるものも数多く存在します.そのようなデータに対して正規線形モデルを当てはめるのは適切ではありません.このような不都合に対して,考案されたのが一般化線形モデル(Generalized Linear Model; GLM)です.
本記事はpythonでの実行例の紹介がメインであるため,GLMの数理的な説明は割愛し,ざっくりとしたイメージのみを説明します.GLMの詳細に関しては,別記事を作成するかもしれません.
GLMは,先ほどの正規線形モデルの線形予測子(\(x^t\beta\))を用いて,応答変数の期待値\(E(Y):=\pi\)をリンク関数\(\mu(\cdot)\)により変換したものを説明する下記のモデルを想定します.
$$\mu(\pi) = x^t\beta$$
上記の式で,\(\mu(\cdot)\)の逆変換を考えると,
$$\pi = E(Y) = \mu(x^t\beta)^{-1}$$
となります.ここで逆変換\(\mu(\cdot)^{-1}\)が\((0,1)\)や\((0,\infty)\)をとるように適切に\(\mu(\cdot)\)を設定できれば,応答変数の範囲がおかしい!という問題は解消されます.説明変数の線型結合をうまいこと変換して応答変数の範囲を変化させたのがGLMのアピールポイントです.
補足:ポアソン分布
(ここは,読み飛ばしていただいて構いません.)
ポアソン分布は,下記のような確率関数を持つ分布で\(Po(\lambda)\)と表すことにします.
$$f(x) = e^{-\lambda}\frac{\lambda^x}{x!},\ \lambda > 0,\ x = 0,1,2,…$$
この分布はある期間内に平均で\(\lambda\)回発生する事象がちょうど\(x\)回発生する確率と解釈できます.このような解釈のもと,ある期間内の何らかのイベントの発生回数がどれくらいの確率で起こるかのモデリングに利用されます.
ポアソン回帰(対数線形モデル)
ポアソン回帰は,応答変数が計数データの場合に,説明変数と応答変数との関係性をモデリングするために利用されます.対数線形モデルとも呼ばれることもあります.モデル式としては,先ほどのGLMのリンク関数を対数関数\(log(\cdot)\)とした下記になります.
$$\log(\pi) = \log(E(Y)) = x^t\beta$$
もしくは
$$\pi = E(Y) = \exp(x^t\beta)$$
このモデルの係数\(\beta\)を推定することで,範囲が\((0, \infty)\)に制限された応答変数への説明変数の寄与の大きさを算出することができます.モデルの当てはめた後の結果の解釈は,適合度をみたり,係数=0を帰無仮説とした統計的検定をおこなったり,のように通常の重回帰分析とほぼ同じです.
statsmodelsを用いたpythonでのポアソン回帰/対数線形モデルの実行
今回は,Rの”AER”(Applied Econometrics with R)パッケージの”EMES1988″の一部の変数を抽出したデータセットを作成し,分析してみます.このデータは,患者さんの情報とお医者さんの訪問回数を記録したものです.なお,全てのコードはnotebookに記載しており,ここでは,ポアソン回帰の実行に必要な部分のみを抜粋して掲載します.
## 必要パッケージの読み込み等
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.graphics.api import abline_plot
from sklearn.metrics import mean_squared_error
plt.style.use("ggplot")
## statsmodels.api.datasets.get_rdataset()を用いて,RのAERパッケージからEMES1988を読み込む
### 外科医の訪問が要請される回数を予測するデータセット
NMES1988 = sm.datasets.get_rdataset("NMES1988","AER")
df = NMES1988.data[["visits", "hospital", "health", "chronic", "gender", "school", "insurance"]]
## カテゴリ変数を数量に置き換える
df["health"] = df["health"].map({"poor":1,
"average":2,
"excellent":3})
df_dummy = pd.get_dummies(df, columns=["gender", "insurance"], drop_first=True)
## 独立変数と説明変数それぞれのデータフレームを作成
df_X = df_dummy.drop(columns=["visits"])
df_X = sm.add_constant(df_X) # 切片用のカラムを追加
df_y = df_dummy["visits"]
## statsmodels.api.GLM()関数を用いたポアソン回帰の実行
pois_reg = sm.GLM(df_y, df_X, family=sm.families.Poisson())
res = pois_reg.fit()
## ポアソン回帰モデルの当てはめの結果(各独立変数の係数やモデルの適合度など)の表示
print(res.summary())以上を実行すると,以下のような結果が得られます.
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: visits No. Observations: 4406
Model: GLM Df Residuals: 4399
Model Family: Poisson Df Model: 6
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -17977.
Date: Mon, 09 May 2022 Deviance: 23178.
Time: 14:24:36 Pearson chi2: 2.94e+04
No. Iterations: 5
Covariance Type: nonrobust
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 1.5774 0.036 43.574 0.000 1.506 1.648
hospital 0.1635 0.006 27.314 0.000 0.152 0.175
health -0.2791 0.015 -18.737 0.000 -0.308 -0.250
chronic 0.1455 0.005 31.848 0.000 0.137 0.155
school 0.0262 0.002 14.233 0.000 0.023 0.030
gender_male -0.1126 0.013 -8.697 0.000 -0.138 -0.087
insurance_yes 0.2040 0.017 12.109 0.000 0.171 0.237
=================================================================================この結果を簡単に解釈するならば,例えば
係数(coef)をみると,全ての係数のP値が0.000であるため,係数=0を帰無仮説とした検定はそれぞれ棄却される.つまり,医者の訪問回数のモデル化に今回組み入れた変数は有用であると判断できる.しかし,適合度として,peason chi2を見てみると,あまりにも大きな値が出ているため,実現値とモデルのあてはまりが良いとは言えない.今回含めた変数群に他の変数を追加するなどして,モデルがよりデータを説明できるよう改良する努力が必要であろう.のような感じになります.物々しい物言いにするとそれっぽくなりますね.
おまけとして,パラメータ推定を行った後のポアソン回帰モデルを用いて算出した従属変数の理論値な可視化をしました.
df_y_pred = pd.DataFrame(res.mu)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hist([df_y, df_y_pred[0]], bins=50, alpha=0.6, histtype="stepfilled")
ax.set_xlabel('the number of physician office visits')
plt.show()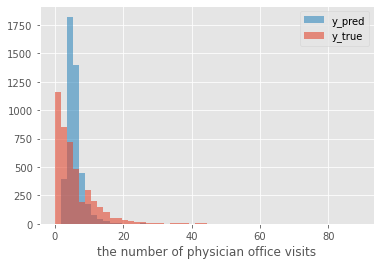
これをみると,実測値と理論値の分布が異なっていることが分かります.実測値が0付近に集中しているのを理論値はうまく反映できていません.これは,元データが0付近に集中している(zero-inflated data)のに対して,ポアソン分布(平均(>0)付近に最も集中する.この例ではこの例では7,8くらい?)を当てはめたことが原因と考えられます.
まとめ
本記事では,下記の2点を紹介しました.
- 応答変数が計数データである場合に利用可能な回帰モデルであるポアソン回帰の概要
- statsmodel.apiを用いて,pythonでポアソン回帰を実行する方法
係数データが応答変数となる場合は多いと思うので,ぜひご活用ください.
References
(notebookはどこで共有すれば良いのか...?検討中.githubに上げるか,googlecolabそのままリンク貼り付けるか?)

コメント