多変量正規分布の確率等高線の書き方(1/4)

本記事について

本記事は，以下の流れで説明する多変量正規分布の確率等高線の書き方についての，全体像を概観するための記事です．特に，何をやろうとしているか？についてのイメージ共有に絞って記載します．

1. 何をやろうとしているか？（本記事）
2. 多変量正規分布の平均ベクトルの統計的仮説検定（別記事：リンクを後で入れる）
3. 実際に書いてみる（別記事：リンクを後で入れる）
4. 読むのに必要とされる数学の補足

前提知識｜多変量正規分布

$p$次元ベクトル$x$が平均ベクトル$\mu$，正定値対称の分散共分散行列$\mathrm{\Sigma }$の多変量正規分布に従う時，

$$x\sim MN(\mu ,\mathrm{\Sigma })$$

と書きます．この時，$x$の確率密度関数(probability density function, pdf)$f(x)$は，以下のように表せます．

$$f(x)=\frac{1}{(2\pi {)}^{p/2}det(\mathrm{\Sigma }{)}^{1/2}}\exp (-\frac{1}{2}(x-\mu {)}^t{\mathrm{\Sigma }}^{-1}(x-\mu )),x\in {\mathbb{R}}^p$$

平均ベクトルが分布の中心の位置，分散共分散行列が分布の散らばりの状況を表しています．今回の一連の記事では，等高線を書くことが目的であるため，分散共分散行列$\mathrm{\Sigma }$が主役となります．

（ちなみに正規分布はこの2つのパラメータで決まることから，多変量正規分布は2次までのモーメントで定まる分布と言えます．）

　試しに，$p=2,\mu =(0,0{)}^t$として，分散共分散行列$\mathrm{\Sigma }$をいくつかかえて散布図を書いてみましょう．

$\mathrm{\Sigma }$が単位行列の場合

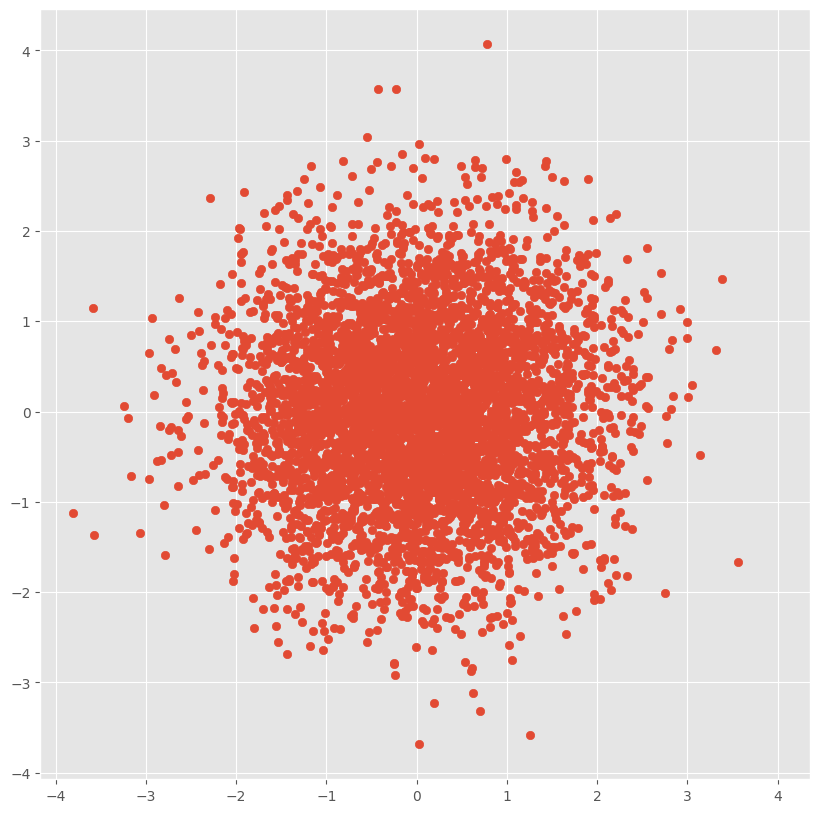
正円のように分布していますね．

$\mathrm{\Sigma }$が単位行列でない対角行列の場合

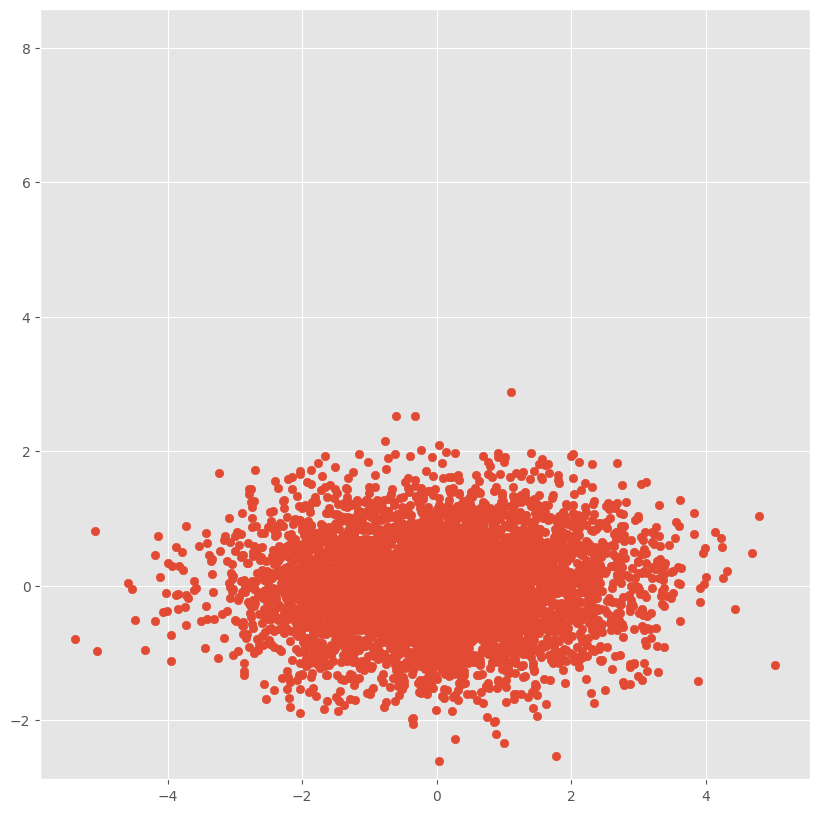
正円を潰したように(=楕円形に)分布していますね．

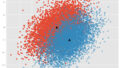
$\mathrm{\Sigma }$が上記以外の正定値対称行列の場合

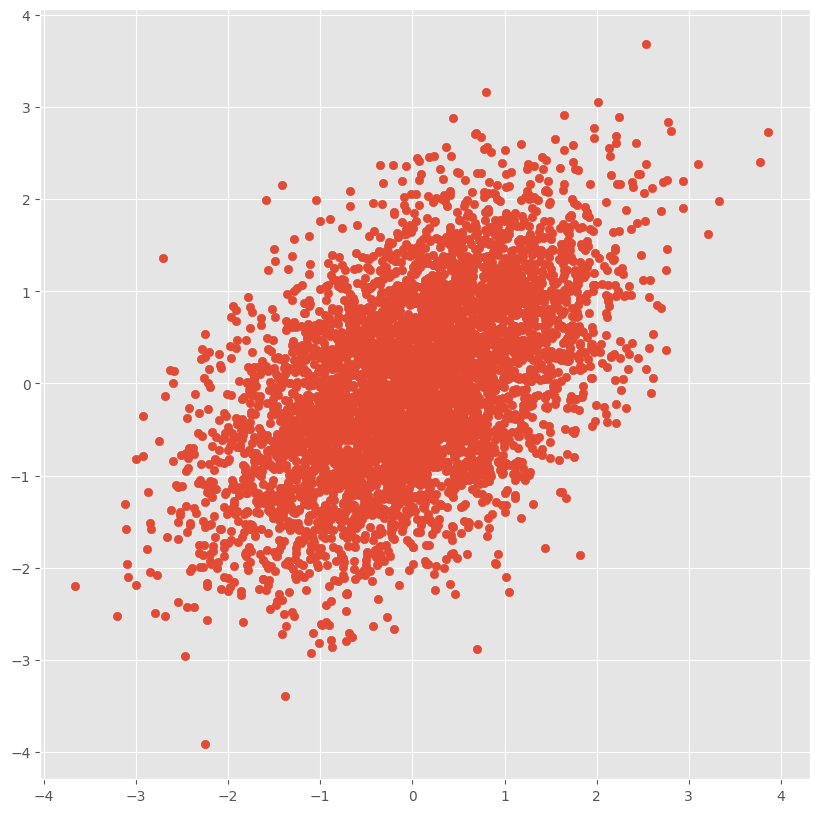
傾いた楕円のように分布していますね．

多変量正規分布の確率等高線のイメージ

この一連の記事では，以下のような図を描画する方法を記載していきます．ここで，確率等高線（青野楕円）は正規分布の平均ベクトルの95%信頼領域の外縁を表しています．

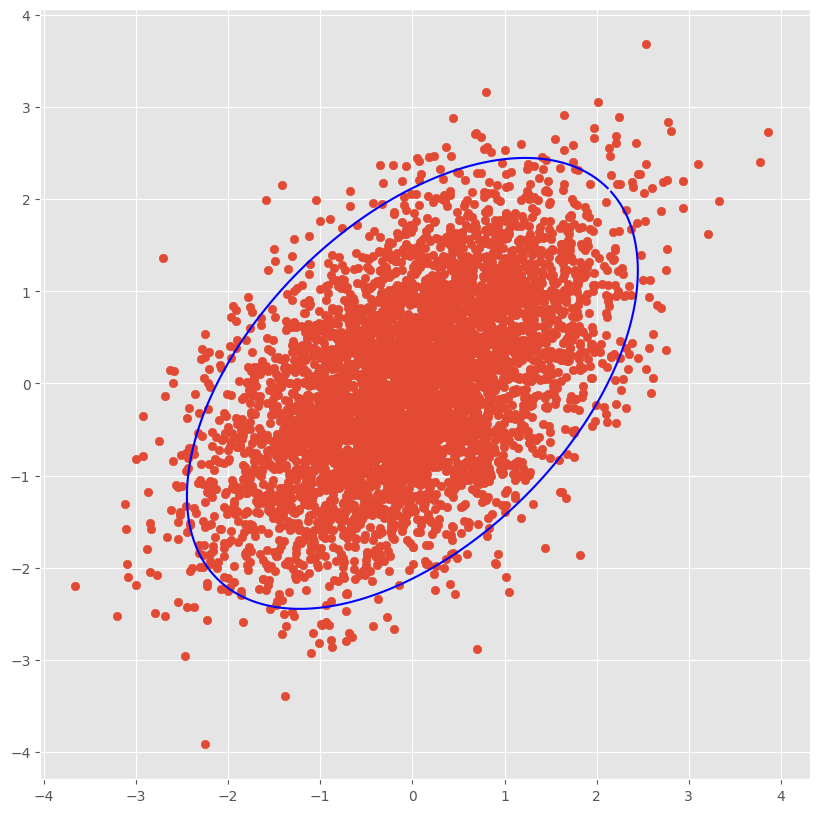
まとめ

本記事では，「多変量正規分布」と「その確率等高線のイメージ」をご共有しました．以降の記事にて，平均ベクトルの検定や，その検定と等高線の関係性について記載していこうと思います．

記事の中での誤りがございましたら，やんわりとご指摘ください．

読者様の参考になると幸いです．